On-chain Verification of the LR Model Training using ZKP

In the last article, we have given a sketch of the full picture of the next generation data trading infrastructure which is built using Privacy-Preserving Computation, Zero-Knowledge Proofs and the Blockchain:

In this article, we will go deeper into a concrete example of the ZKP verification of a Logistic Regression model training task on the Blockchain. Which is also what we have implemented in a recent release of Crynux.
Verification of the Logistical Regression Task.
The computation task is to train a Logistical Regression (LR) model, which is a very basic and popular model used in both machine learning and statistical analytics (to do the Multiple Factor Analysis).
The process of a Logistical Regression task
The LR training process is divided into several iterations. In each iteration, the data holder computes a gradient incremental on the model parameters given as the input. The incremental is then applied to the model parameters, which is used as the input for the next iteration. When the incremental is zero, the model is converged, and the training is completed.
The original data is distributed across multiple data holders horizontally. The PPC method used to do the training is Federated Learning.
The process of a single iteration is illustrated in the figure below:
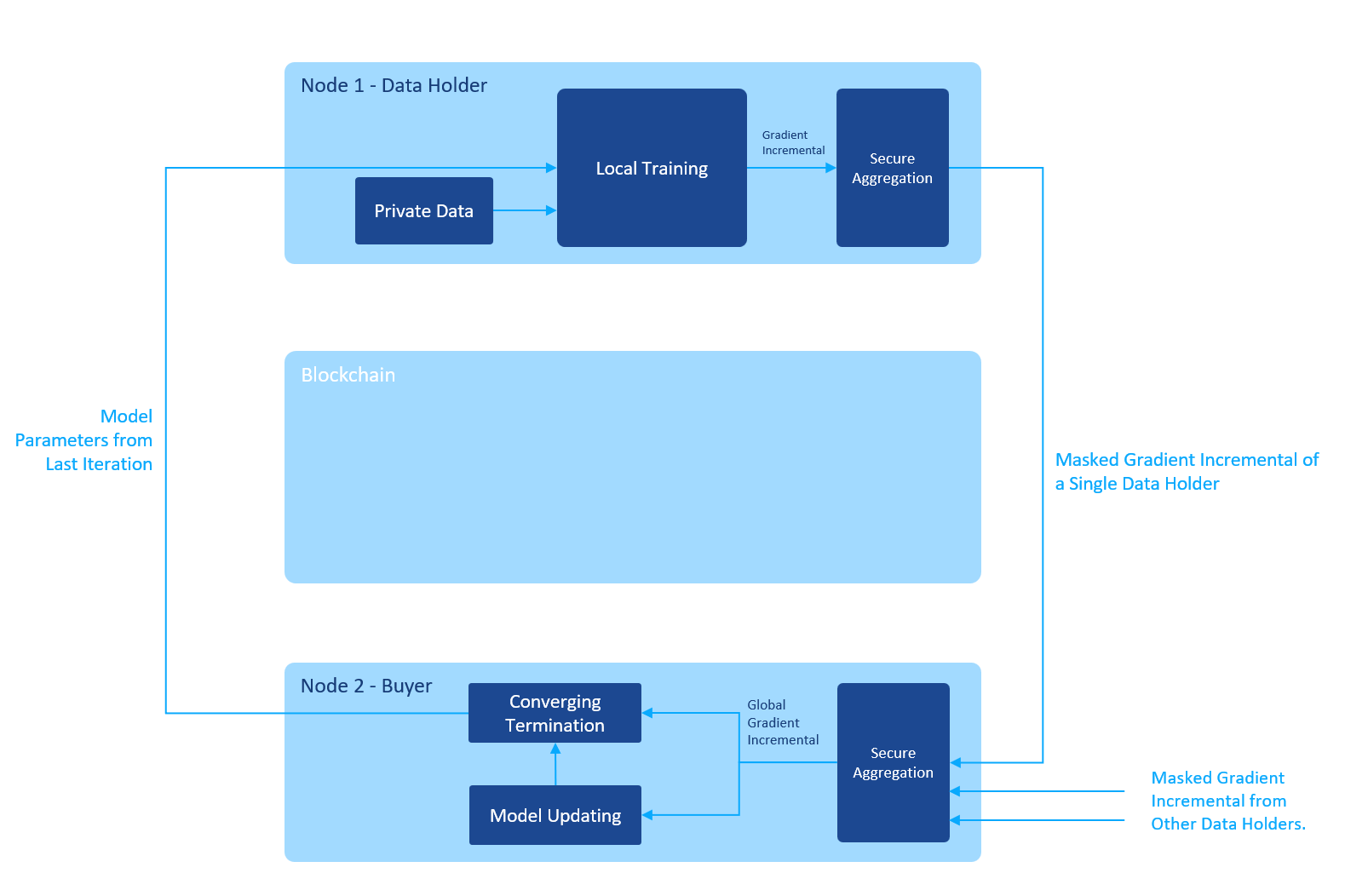
The buyer starts the iteration by sending the initial model parameters to all the data holders. The data holders train the model using their local private data and send the gradient incremental back. Note that the plain text gradient is masked using secure aggregation algorithm before sending out, so that the buyer can only get the global gradient by summing up all the masked gradient from all the data holders. The gradient of a single data holder is never exposed to the outside world.
After getting the global gradient, the buyer applies it to the model parameters, checks if the model is converged, and decides whether to start another iteration or not. When the model is converged, the task is finished:
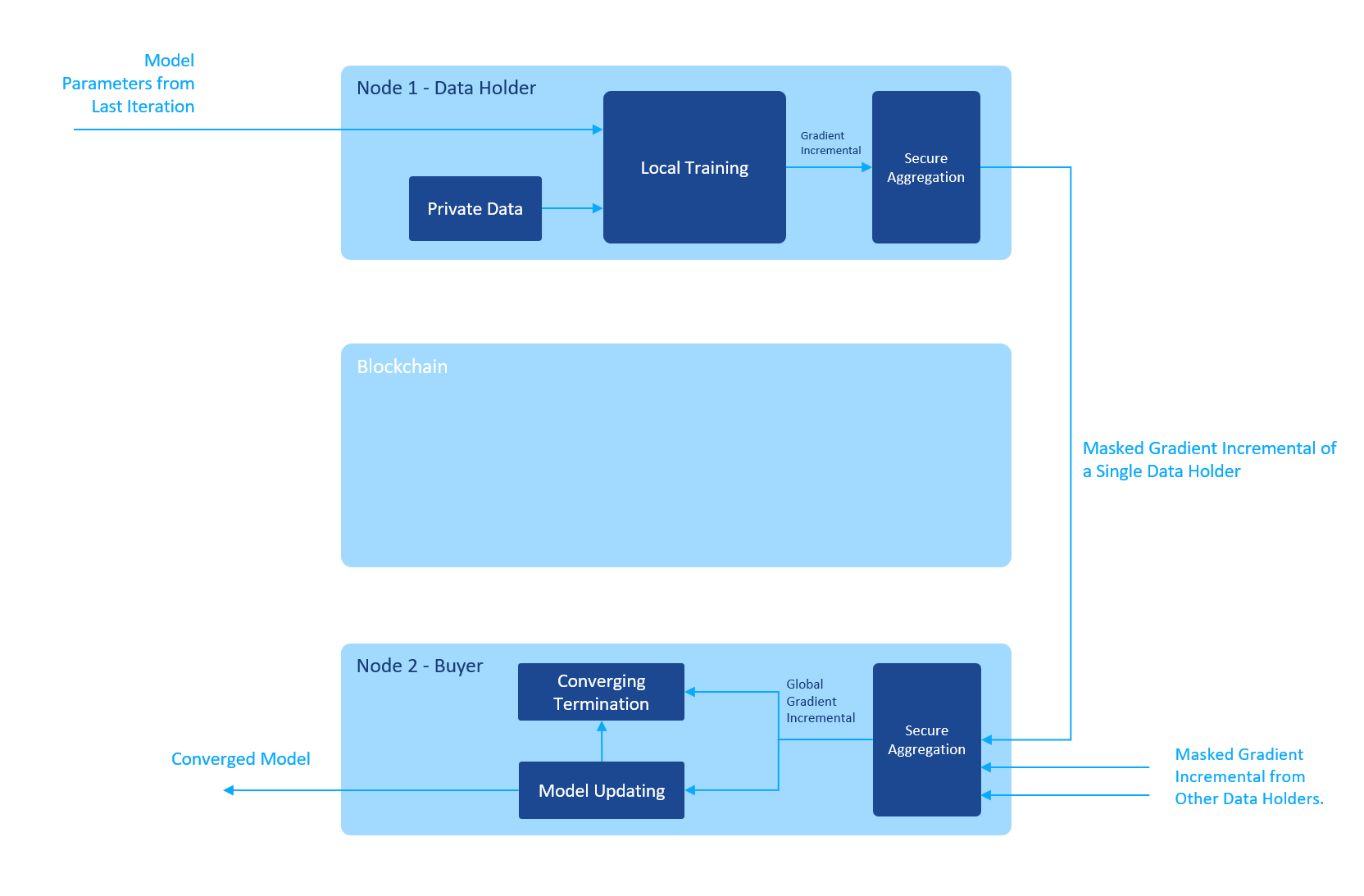
The verification of a Logistical Regression task
To confirm the success of the trading transaction, we must review the transaction from end to end, addressing all the places where one participant has the chance to cheat the other, and design a ZKP verification scheme to avoid it.
From “computation verification” to “convergence verification”
Let’s start by examining the computation process, which contains a varying number of iterations, with each iteration starting from the private data and the initial model parameters, and ending with the masked gradient.
Wait, the mask is generated during several rounds of communications between the data holders using asymmetric cryptography. Which is by design of the Federated Learning. To include the mask generation process in the ZKP is already a mission too complex to finish. Even if we finish the design, it will make the ZKP generation too slow to be practical.
That leads us to think in a different direction, which is the convergence process. The idea behind is that the only one thing the buyer cares about is to get a converged model on the data he requires. If the model is converged, and the data is used, he is satisfied. No other information such as the number of iterations is needed.
The model should be converged
To prove to the buyer that the parameters he received is converged, the data holder must generate a ZKP for the computation of one more iteration, where the input is the converged model parameters, and the output is the gradient. Since it is done for only one iteration, exposing the gradient to the public won’t cause any privacy issues. We can safely ignore the masking process and reveal the gradient in the ZKP so that the Blockchain could sum up the gradient from all the data holders to check whether it is converged or not.
This greatly reduces the amount of work required to generate the ZKP. Only one ZKP is required for a task instead of an iteration. The PPC steps are removed from the ZKP generation. We’re even adding the possibility to use one ZKP scheme to support all kinds of PPC algorithms.
The data should be used
As we have discussed earlier in this article, there is no way for the Blockchain, or anybody else who has no access to the plain text data, to verify the original data is not fake. We are implementing a data sourcing mechanism to leave the evidence so that one day, the buyer may ask for an audit on a previous task, and he can be sure that the data passing the audit was the data used in the computation.
The implementation is simple. By calculating the hash of the original data in the computation steps, and including the hashing process in the ZKP, revealing the hash value as the public output, the ZKP has the ability to prove that the result is from the data with certain hash values.
Missing Point 1: The converged model should be received by the buyer
We were seeing the verification process from the buyer’s perspective. If we’re going to verify the task on the Blockchain, a different thing is that the Blockchain doesn’t have the final converged model parameters. We were assuming that the buyer received the parameters and then started the verification. Since the parameters are not visible to the Blockchain, nor are they revealed in the ZKP. The data holders have a chance to send the correct ZKP to the Blockchain without sending the parameters to the buyer. How could the Blockchain be sure that the buyer actually gets the computation result he paid for? Or, what if the buyer claims he does not get the result when he actually got it?
To design the proof of model reception, we must go back to review the last training iteration where the buyer sends the initial model parameters to the data holders and in the end get the global gradient from the data holders.
Since this is the last iteration, the model is converged. Which means the global gradient is zero (or near zero below a given threshold). Which means the initial model parameters given as the input by the buyer are the same as the final converged ones! Which means the buyer has already got the final result before the last iteration! Bingo!
As the Blockchain, we ask the buyer to submit the hash of the initial model parameters to the Blockchain when initiating an iteration. And in the ZKP, the data holders calculate the hash of the input parameters as well and reveal it as the public output. The Blockchain could then verify that the hash of the converged model parameters is the same as the one submitted by the buyer. And since the buyer could generate the hash of the converged model parameters, he must have the original values of the parameters.
Missing Point 2: The ZKP and the task should be relevant
Another way for the data holder to cheat is to reuse the ZKP of a task to pass the verification of another task.
Technically the ZKP generation & verification methods are different for different computation tasks. When the buyer submits the task to the Blockchain, he should also submit the corresponding ZKP verification method to the Blockchain so that the Blockchain could use the correct verification method to check the ZKP.
The data holder however, before executing the task, should also check the correctness of the verification method on-chain in case that the buyer submits an invalid verification method that he could never pass.
We have finally completed the design of the ZKP scheme. The figure below shows the complete design of the ZKP scheme:
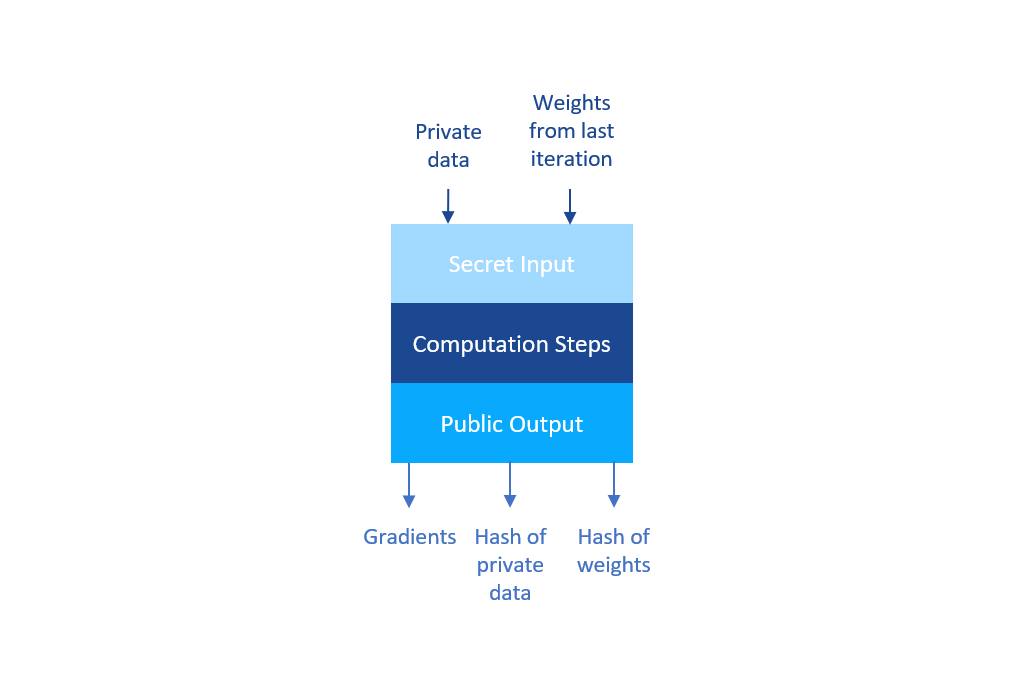
And below is the workflow of a complete iteration of the LR training including the ZKP related steps:
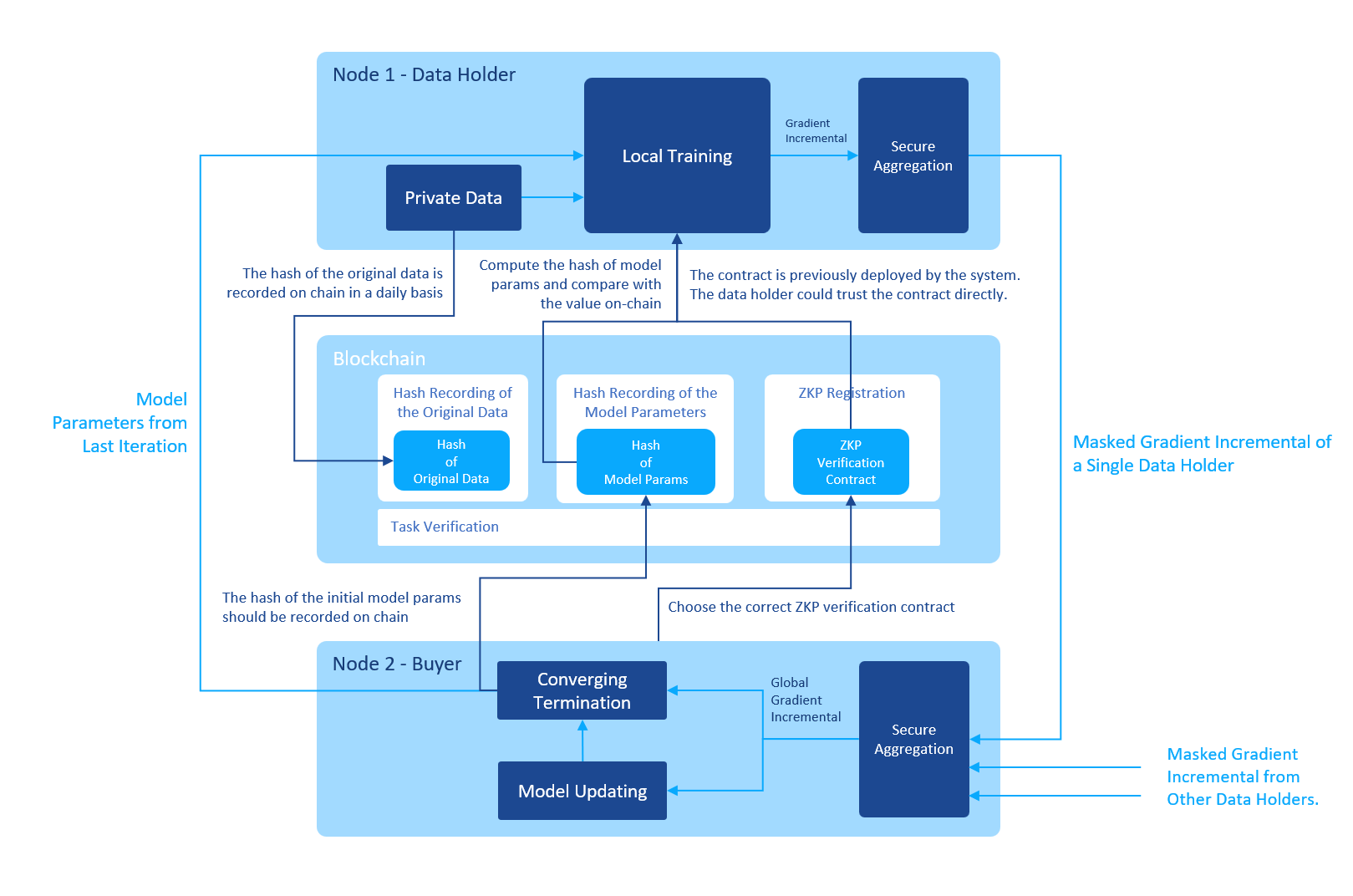
When the buyer starts the task, he selects the right verification contract to use, saves the selection in the task config and submits the task config to the Blockchain.
Then the iteration begins. For each iteration, the buyer calculates the hash of the initial model parameters and submits the hash to the Blockchain. After receiving the hash, the Blockchain notifies the data holders to start the iteration.
The data holder fetches the hash from the Blockchain, retrieves the initial model parameters from the buyer, hashes it and compares the value with the value from the Blockchain. If the values are different, the data holder won’t start the calculation since he knows that he will not be able to pass the ZKP verification on-chain.
The data holder then performs the training using the local private data, whose hash values have already been submitted to the Blockchain before. If the hash values are not on-chain, the verification later won’t pass.
After the training, the data holder sends the masked gradient to the buyer and finishes the iteration.
If the buyer finds out that the model is converged, he could start the verification process. If the buyer is malicious, he could also stop here, refuse to participate in any future steps since he has got the model already. In this case the verification process could as well be started by the data holders. As long as the verification passes, the data holders could get paid by the Blockchain using the money (tokens) prepaid by the buyer on-chain.
The verification process of the Blockchain is shown in the following figure:
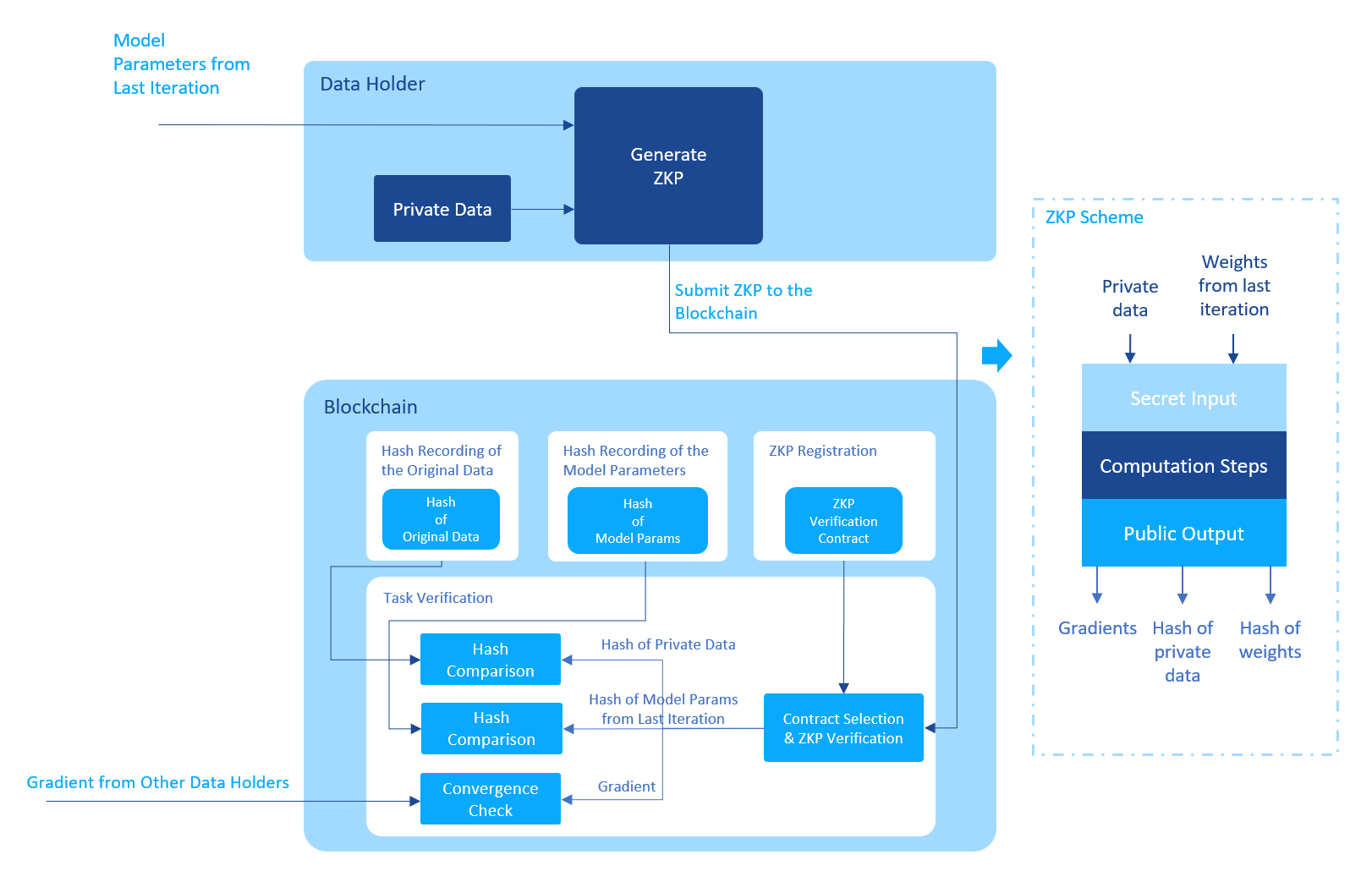
After receiving ZKP from the data holder, the Blockchain selects the verification contract that is specified in the task config, uses the contract to verify the correctness of the ZKP.
If the ZKP passes the verification, the Blockchain further extracts the public outputs from the ZKP. And checks the correctness of the outputs:
- The hash of the private data is the same as the hash recorded on-chain.
- The hash of the model params of the last iteration is the same as the hash recorded on-chain.
- The gradient, summed up with the gradients from other data holders, bellows a preset threshold.
If all the checks have passed, the Blockchain is confident that the task has finished successfully.
The design of the whole process of the ZKP verification of the LR task is completed.
Note that this article is still just a high-level description of the whole process. To implement it is a completely different story. Too many minor details must be taken care of. Such as the implementation of floating-point computation and the sigmoid function inside ZKP, and the ZKP-friendly hashing function MIMC7.
There are still some problems left though. When the model is not converged after the training, if the data holder cannot prove that he did spend computing power on the training, could he still get paid? If one of the data holders fails to submit the ZKP, could others get paid?
And the ZKP generation is still slow even after all these optimizations. If the dataset is large, we can hardly say that the above implementation is practical. We believe that the development of new ZKP protocols will solve this problem in the future.